[데이터 통신] 나이퀴스트 비트율, 섀넌 용량

데이터 속도의 한계 ( Data Rate Limit )

데이터 통신에서 고려해야 할 점은 "채널을 통해 초당 비트수로 데이터를 얼마나 빨리 보낼 수 있는가"이다. 이러한 데이터 속도를 계산하기 위해 두 가지 이론 공식이 개발되어 있다. 하나는 잡음 없는 채널에 사용하는 Nyquist 나이퀴스트 수식, 잡음이 있는 채널에서 사용하는  Shannon 섀넌 수식이다.

 

Nyquist 나이퀴스트 비트율 -무잡음 채널-

bandwidth : 대역폭, L = 데이터를 나타내는데 필요한 신호레벨, BitRate :초당 비트 수

Shannon 섀넌 용량 - 잡음 채널 -

사실 잡음 없는 채널은 없다. 1944년에 Claude shannon은 Shannon 용량이라는 공식을 도입하여 잡음이 존재하는 시스템에서 보낼 수 있는 최대 데이터 속도(최대 전송률)를 구했다.

bandwidth = 대역폭, SNR = 신호에 대한 잡음 비율, capacity = bps 단위의 채널 용량

이 수식에서 주목할 점은 수식에 신호 레벨(L)이 들어가지 않는다는 것이다. 이는 레벨 수를 아무리 늘려도 일정 한계이상의 전송률을 달성할 수 없다는 것을 의미한다.

(사실 현실에서는 어떤 신호 레벨과 어떤 대역폭이 필요한지 알기 위해 두 가지 방법을 모두 사용한다)

 

 

노이즈가 너무 커 SNR 값이 거의 0인 경우, Capacity는 다음과 같이 정의한다. 

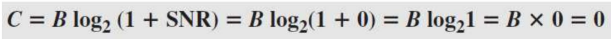
위 수식은 채널의 용량은 대역폭에 관계없이 0임을 의미한다. 이러한 경우 이 채널을 통해 데이터를 수신할 수 없다.

 

 

예를 들어 수식을 적용해보자

bandwidth(대역폭)가 1 MHpz인 채널이 있다. SNR 값은 63일 때, 비트율과 신호레벨을 구하라

잡음이 있는 채널의 상한을 구하기 위해 섀넌 용량 공식을 사용하여 상한이 6 Mbps임을 알았다. 하지만 더 좋은 성능을 위해 4 Mbps로 정하자.

그 후 나이퀴스트 정리로 신호레벨(L)을 구할 수 있다. 위 식에서 4 레벨로 채널 신호를 구성하면 된다.